1. Teil der Trilogie: Ein verliebter Rundweg
(Published on 28. September 2010, 12:34 by berni)
Instructions: Blacken some of the hitori fields (bordered pink) in the diagram, that in every row and every column every sum
– to be explained shortly – appears at maximum once. All fields that are not blackend have to be connected (that is, the black fields may not depart the puzzle into two or more pieces). No two black fields may be connected horizontally or vertically.
Draw a single continuous loop by connecting neighboring dots along the dotted lines. The numbers indicate how many edges of a cell are used for the loop. The loop may not touch or cross itself, and it doesn't need to touch all of the dots. Numbers in blackend hitori fields do not count (they can be true or false). All blackend hitori fields are outside of the loop.
Now you can calculate the sum
mentioned above. This is the sum of all given numbers inside of the loop, including all the numbers inside of the loop, that are hidden with small gray squares – for this numbers you have to count the number of edges of the cell.
PS: If within a hitori field there is no number inside the loop, the sum is, as usual in math science, zero.
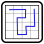
Small Example: In the solution everything thats pink belongs to the hitori and everything thats black belongs to the loop.
Solution code: The sizes of the areas outside of the path (inclusive hitori cells), clockwise starting at top left.
Comments
on 30. July 2024, 12:22 by Las4one
Penpa: https://tinyurl.com/27svk7cr
on 23. August 2023, 19:42 by Agent
Sehr schön, danke!
on 27. July 2023, 23:27 by Myxo
Wunderschönes Rätsel!
on 26. November 2018, 12:34 by berni
Nicht mehr funktionierende Links entfernt.
on 6. September 2018, 11:00 by jessica6
Sehr schöne Kombination. Mein 1000. gelöstes Portalrätsel!
on 24. September 2014, 07:41 by AnnaTh
Wie konnte ich so ein schönes Rätsel so lange ignorieren?
on 9. September 2014, 21:43 by Krokofant
Hat zwar recht lange gedauert, aber super schön zu lösen!! :) Beeindruckend, danke!
on 4. May 2014, 22:50 by ch1983
Auch in 2014 sehr lösenswert, danke!
(Schon die Geschichte der Liebenden drumherum ist klasse!)
on 15. August 2013, 08:22 by Statistica
Eigentlich für ruhige Urlaubsstunden gedacht, musste das Rätsel nun doch etwas länger liegenbleiben. Wenn man sich erst einmal reingedacht hat, gar nicht mal sooo schwierig. Klasse.
on 31. December 2012, 15:22 by Mody
Bestimmt schon zehnmal "in Angriff genommen" und endlich endlich ohne Widerspruch durch.
Was für ein großartig, superschön konstruiertes Rätsel :)
on 17. February 2011, 20:43 by Phip
Ein wirklich tolles Rätsel!! Zuerst wollte ich mir dieses nicht antun, aber dann hat's mich gepackt, und Schritt für Schritt ging's vorwärts. Mit der Zeit war ich richtig angefressen... Vielen Dank!!
on 30. September 2010, 07:09 by SilBer
Ein wunderschönes Rätsel, Berni! Hat mich vom Lösungsweg an die Lügner-Rundwege erinnert... Aber das Thema gefällt mir noch ein bisschen besser! ;-) LG Silke
on 30. September 2010, 00:54 by ibag
Waaaahnsinn! Hat mich allerdings 4 Anläufe gekostet. Aber sie waren mir tatsächlich alle 4 ein Vergnügen (vor allem der letzte)!
on 29. September 2010, 03:20 by Le Ahcim
Das Ding mit dem Zählen sollte ich noch mal üben... war auf der Zielgeraden kurz vor'm Nervenzusammenbruch.
Ansonsten ein spitzen Berni-Alles-In-Einem-Rätsel der Extraklasse. Möchte gar nicht wissen, wie lange die Konstruktion dieses Hammers gedauert hat, geschweige denn, wie lange hier der/die Testlöser(in) dran saß(en)...
on 29. September 2010, 01:48 by Alex
supertoll (Idee, Konstruktion und alles)! Konnte es einfach nicht ueber Nacht liegen lassen...
on 28. September 2010, 23:34 by pokerke
Wow, great puzzle!
It took me all evening, but it actually works quite logically one small step at a time.
I can't imagine how you start to build a puzzle like that.
on 28. September 2010, 18:36 by Le Ahcim
Oh man... Jetzt, dank Beispiel, weiß ich, wo bei mir der Haken war...
on 28. September 2010, 18:27 by berni
Kleines Beispiel hinzugefügt.
on 28. September 2010, 16:31 by Mody
Mir ist auch noch nicht klar, ob die Umrandung eines Schwarzfeldes als Kante gesehen wird, wenn an das Schwarzfeld ein Rundwegaußenfeld grenzt.
@Mody: Mir ist nicht ganz klar, was du meinst, aber alle Kanten zählen als Kanten, auch die von Schwarzfeldern.
on 28. September 2010, 15:46 by Luigi
Hm... ich habe da doch ein paar Verständnisprobleme.
Es können also nur geschwärzte Felder "falsch" sein.
Diese können jedoch irgendwie falsch sein und nicht nur "knapp daneben"?
@Luigi: Genau!
on 28. September 2010, 15:03 by Statistica
Mach mal. Dann aber bitte auch mit dem Label: "Passt beim Ausdruck auf ein DinA4-Papier und ist auch noch lesbar" :-)
on 28. September 2010, 14:23 by berni
Jörg: Ist das etwa eine Herausforderung?!? Naja, ich glaube, Computergeneriert, für Anfänger geeignet und Optimierer sollte man ausklammern, dann hat man, denke ich mal, eine Chance, wirklich alle anderen zu verwenden...
on 28. September 2010, 14:11 by Statistica
Hübsch. Da denke ich dran, dass ich AUCH mal meinen Schreibtisch aufräumen sollte ;-). Und eine richtige Labelparade. Ich warte nur auf das erste Rätsel, für das ALLE Label verwendet werden können (Nein! Tut es nicht!)
on 28. September 2010, 13:31 by Mody
Gelten die kleinen grauen Quadrate als geschwärzte Felder
oder sind sie grau, einfach weil grau hier farblich hübsch aussieht :)
@Mody: Die grauen Quadrate sind im Text immer als graue Quadrate bezeichnet und nicht mit den geschwärzten Hitorifeldern zu verwechseln. Grau hatte ich gewählt, weil man dann beim Ausdruck auf dem Feld was notieren kann, beispielsweise die Zahl, die dieses Quadrat verdeckt.