九章线性代数
(Eingestellt am 5. Februar 2026, 17:59 Uhr von MOD)
English:
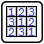
1. Row Rule: Each row is a permutation of the vector C1=(1,2,…8,9).
2. Column Rule: Each column is a permutation of the transpose of the vector C2=(1,2,…8,9).
3. Submodules: The entire 9×9 grid is partitioned into 9 non-overlapping 3×3 submatrices. Among these, 8 are invertible matrices, and 1 is a singular (non-invertible) matrix. Each submodule contains distinct numbers with no repetition.
4. Rank Constraint: The rank of the singular 3×3 submatrix is equal to the number that should be placed in the cell marked with "?". Furthermore, this number must not appear in the same relative position across all 9 submodules. (For example, if the rank of the singular matrix is n and the top-left cell of a submodule is n, then the top-left cell of every other submodule cannot be n.)
5. Inversion Count Rule: The numbers outside the grid indicate the number of inversions in their corresponding row or column vector.
6. Core Matrix Constraint: There exists a 3×3 matrix A=(aij) that is orthogonally adjacent (horizontally or vertically) to the singular matrix from Rule 4, satisfying:
- The determinant of A, det(A), equals a33.
- The tens digit of the determinant of the adjugate matrix det(A*) is a32, and the units digit is a23.
- Let B=(bij) be the square matrix formed by the minor of a33 in det(A). Then the product of det(B^(-1)) (the determinant of the inverse of B) with b12 and b22 must both be integers.
7. Matrix Transpose and Submodule Correspondence: Each element (A^T)_{i,j} in the transpose of matrix A (which is aji in the original matrix A) must equal the element in the corresponding position of all submodules from Rule 3.
- Example: The element in the 3rd row, 2nd column of the 3rd submodule from the top and 2nd from the left equals a23 in matrix A (i.e., (A^T)_{3,2}).
Chinese:
1.行规则:每行数字为向量C1=(1,2,…8,9)的一个置换。
2.列规则:每列数字为向量C2=(1,2,…8,9)的转置的一个置换。
3.子模块:整个9×9网格可划分为9个互不重叠的3阶矩阵,其中8个为可逆矩阵,1个为不可逆矩阵;每个矩阵内无重复元素。
4.秩约束:该不可逆3阶矩阵的秩,等于“?”位置应填的数字;且该数字在所有9个子模块的相同相对位置上均不重复(例如,若不可逆矩阵的秩为n,且已知R1C1为n,则每个子模块的第1行第1列元素都不能是n)。
5.逆序数规则:网格外的数字,对应其所在行或列向量的逆序数。
6.核心矩阵约束:存在一个与规则4的不可逆矩阵正交相邻的3阶矩阵A=(aij) ,满足:
- 矩阵的行列式det(A) = a33;
- 其伴随矩阵的行列式det(A*)值的十位数为a32,个位数为a23;
- 记其行列式的a33的余子式构成的方阵为B=(bij) ,则B的逆矩阵的行列式det(B^(-1))与b12、b22的乘积均为整数。
7.矩阵转置与宫格对应:规则6中矩阵A的转置A^T中每个元素(A^T)_{i,j} (即原矩阵A的元aji),与规则3中所有子模块的对应位置元素相同。
- 示例:从上往下数第3个、从左往右数第2个子模块的第3行第2列元素,等于A的元素a23(即(A^T)_{3,2})。
Lösungscode:
Kommentare
am 6. Februar 2026, 14:27 Uhr von marcmees
solution code is Chinese to me.
am 6. Februar 2026, 13:55 Uhr von luoji
Where's the solution code.
By the way, novel rules, though hard for manual work:)
am 6. Februar 2026, 11:31 Uhr von MOD
发现不唯一解
am 6. Februar 2026, 06:04 Uhr von MOD
Added puzzle image and external solving link.
加入了图片和超链接
am 5. Februar 2026, 18:15 Uhr von MOD
原来这个网站不能加表情包!那些????是被隐藏的表情包
Turns out this website doesn't support emojis! Those question marks (????) are actually the hidden emojis that got blocked.
Es stellt sich heraus, dass diese Website keine Emojis unterstützt! Diese Fragezeichen (????) sind eigentlich die versteckten Emojis, die blockiert wurden.
am 5. Februar 2026, 18:12 Uhr von MOD
新添了链接指引
am 5. Februar 2026, 18:06 Uhr von MOD
Added solving link to Sudokupad