Lost Arrow (Cubedoku)
(Eingestellt am 11. Januar 2025, 16:45 Uhr von Chilly)
This is the latest puzzle in my Cubedoku series. You can find the first puzzle, here, the second puzzle here, and the third puzzle, here.
This one involves arrows, but one of them is 'lost' as it moves onto one of the back faces before re-appearing. You'll need to figure out what it's doing on the invisible face to solve the puzzle. I set this one some time ago, but based on more recent feedback it's not as tricky as I thought so I'm setting it at 3*.
This one involves arrows, but one of them is 'lost' as it moves onto one of the back faces before re-appearing. You'll need to figure out what it's doing on the invisible face to solve the puzzle. I set this one some time ago, but based on more recent feedback it's not as tricky as I thought so I'm setting it at 3*.
Lost Arrow
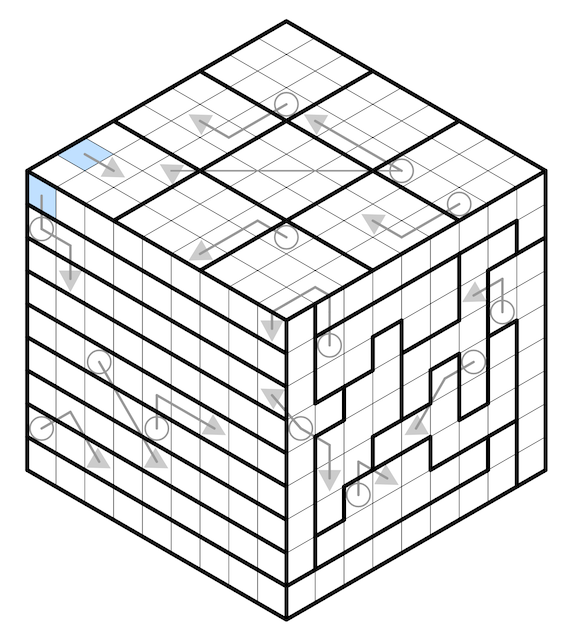
by Chilly
The Rules:
- Fill the cells with the digits 1-9, so that each face of the cube is a valid Sudoku grid. Every digit in each grid indexes a 1x1x1 target cell within the cube, and each target cell must be indexed by all three grids.The digit 1 in a cell specifies that the target cell is the 1x1x1 cube closest to the surface of the cube where the digit is located, whereas a digit 2 in a cell indicates that the target cell is the second cube down from the surface, and so on.
- Normal arrow rules apply. The digit in a circle is the sum of the digits on its corresponding arrow.
- Squares where arrows move onto or off one of the cube faces that is not visible are marked in blue. The blue squares must be joined by the arrow on the invisible face, and the arrow may proceed orthogonally or diagonally in the same way as normal arrows. The invisible face must be a valid Latin square, but may have any valid Sudoku regions.
- Fill the cells with the digits 1-9, so that each face of the cube is a valid Sudoku grid. Every digit in each grid indexes a 1x1x1 target cell within the cube, and each target cell must be indexed by all three grids.The digit 1 in a cell specifies that the target cell is the 1x1x1 cube closest to the surface of the cube where the digit is located, whereas a digit 2 in a cell indicates that the target cell is the second cube down from the surface, and so on.
- Normal arrow rules apply. The digit in a circle is the sum of the digits on its corresponding arrow.
- Squares where arrows move onto or off one of the cube faces that is not visible are marked in blue. The blue squares must be joined by the arrow on the invisible face, and the arrow may proceed orthogonally or diagonally in the same way as normal arrows. The invisible face must be a valid Latin square, but may have any valid Sudoku regions.
The rules are a little complicated, so I'm including the first picture below (courtesy of Andrewsarchus) to show how it works. You can see that entering a digit on one face of the grid determines which single internal 1x1x1 cube is indexed (the target cell), and that cube has to be indexed by all the other faces, putting a further digit on all the remaining faces. There are three visible faces, the digits on all of which are constrained by their indexing connections to the internal 1x1x1 cubes, but also to any Sudoku constraints we place on the surfaces of these faces (e.g. irregular regions, thermos or other standard Sudoku variants). This can lead to some new and interesting interactions. To solve the puzzle, we need to place digits in all cells of the three visible faces. If the faces are 4x4, we use the digits 1-4, or if they are 6x6 we use the digits 1-6, etc. just like normal Sudoku puzzles.
Lösungscode: The first 17 cells along the perimeter of the top face in clockwise order beginning at the top of the image. (17 digits, no spaces)
Zuletzt geändert am 25. Januar 2025, 01:07 Uhr
Gelöst von marcmees, Silverstep, Andrewsarchus
Kommentare
Zuletzt geändert am 12. Januar 2025, 10:47 Uhr
am 12. Januar 2025, 07:15 Uhr von Silverstep
Nice and easy puzzle. 2-3 stars for difficulty.
Yeah - I changed the difficulty - it's not as hard as it looks.
Zuletzt geändert am 12. Januar 2025, 10:46 Uhr
am 11. Januar 2025, 20:28 Uhr von marcmees
Nice ... but never considered the invisible face. Once you get the ball rolling, the puzzle solves very smooth. (3-4*) Thanks
Thanks for the solve - yeah seems like everyone agrees it's easier than it looks.




