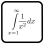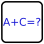The Prime Cages
(Eingestellt am 19. Juni 2023, 22:40 Uhr von I_love_carrie273)
Normal sudoku rules apply. Digits in each cage read left to right or top to bottom form a prime number which contains a sequence of digits equivalent to the cage sum. For example, a cage could contain digits 1, 5, 2, 8, 3, and 9 in this order because 152839 is a prime number and it contains a sequence 2, 8 which forms a number 28 equivalent to 1+5+2+8+3+9. 152389 would be incorrect: it is still prime but there is no sequence 28 (they are separated by 3). Each digit from 1 to 9 must appear in at least one cage. The pairs of cages marked with the same letter sum up to the same number. All the possible pairs were marked and A, B, and C are all different. The sums of non-marked cages are unique and different from A, B, and C. The white dot separates consecutive digits. The black dot separates digits with a ratio 2:1. Not all dots are given.
Lösungscode: The second row left to right followed by the third column top to bottom (18 digits, no spaces)
Kommentare
am 21. September 2023, 19:17 Uhr von Ragna
Super clever ruleset! Fun puzzle. Thank you for sharing. :-))
am 21. Juni 2023, 14:30 Uhr von I_love_carrie273
It all depends on the order of deductions. I knew there is no 8 in other cages before filling anything in: it's not in a 1-cell cage because it is complex; it's not in a 3-cell cage because a cage must not sum up to 18; and it's not in a 4-cell cage because it must sum up to something between 13 and 19 so the remaining digits must sum up to 9 and 8+1 pair is disqualified due to repeating a 1.
am 21. Juni 2023, 12:38 Uhr von sanabas
reason i didn't use that intended logic is because that 5-cage must have a sum starting with 2, and its position is forced by the time you know there's no 8 in other cages. And as the 3 cells that aren't the sum must add to 18, once the 2 is placed the 3 digits that add to 18 are also forced, and include an 8.
am 21. Juni 2023, 08:05 Uhr von I_love_carrie273
The intended logic behind the rule that every digit must appear in at least one cage was to deduce that the 5-cell cage must contain an 8 because it cannot go in any other cage.
am 20. Juni 2023, 18:18 Uhr von I_love_carrie273
Thank you, SenatorGronk :-) As of consulting I think this depends on which numbers can one by heart identify as prime. For example, a single cell cage can be filled only if you either consult tables or know one digit primes by rote.
am 20. Juni 2023, 16:53 Uhr von SenatorGronk
I also didn't need to consider having every digit in a cage. Also, I think it's worth pointing out that this can be solved without having to consult tables of prime numbers.
am 20. Juni 2023, 11:34 Uhr von I_love_carrie273
Thank you, Bankey :-) I used this clue to help me construct the puzzle, besides it just seems elegant, and my solution uses this indeed (but, on the other turn, it allows me to first place digits and then check whether the big number is prime rather than other way round).
am 20. Juni 2023, 10:44 Uhr von Bankey
Fun puzzle. Thanks, @ I_love_carrie273 :). By the way, i didn't need to use the clue about all the digits from 1 to 9 appearing at least once in the cages.