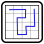
Dueling Pentosnakes
(Eingestellt am 7. Juli 2021, 21:48 Uhr von Nordy)
This puzzle draws inspiration from one of my all time favorite puzzles, Pentosnake by Nikolai Belohuv, and the rules are similar. (CTC solve video)
You must draw two snakes in the grid, where each snake is a 1 cell-wide path that cannot touch itself orthogonally. However, the snakes can touch each other orthogonally. The three circled cells are the ends of the snakes, such that two of the circled cells belong to one of the snakes, and one of the circled cells belongs to the other snake. The remaining end must be found by the solver.
All cells that are not part of a snake must be part of a pentomino. The pentominoes cannot touch orthogonally but can touch diagonally. A letter in a cell represents the pentomino shape that the cell belongs to, and as such lettered cells cannot be used by the snakes. Pentomino shapes of the same letter cannot be repeated in the grid (there cannot be two “L” shaped pentominoes, for example).
Pentominoes for reference:
You can solve on Penpa+ (color pentominoes gray for answer check).
Lösungscode: The length (number of cells) of the shorter snake followed by the number of pentominoes in the grid.
Kommentare
am 15. März 2022, 05:30 Uhr von Nordy
NOTE: This puzzle does have a unique solution, but the solution path requires too much bifurcation (I overlooked a possible configuration). I will be updating this puzzle with better clues.