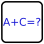Mahna Mahna
(Eingestellt am 16. Juni 2021, 17:52 Uhr von matt383)
Tile the grid so every cell is part of an omino. Use all 12 different pentominoes, all 5 different tetrominoes and a single monomino. Ominoes can not overlap, and digits can not repeat within an omino. The sum of the digits in each omino is given below. (The image does not necessarily show the correct orientation of the ominoes, they can be mirrored or rotated.)
Whenever a single omino spawns multiple boxes, a white dot is given where the omino crosses the edge. The two cells connected by the white dot must contain consecutive numbers.
Pentominoes:
F = 19, I = 19, L = 29, N = 29, P = 32, T = 24, U = 35, V = 24, W = 22, X = 15, Y = 30, Z = 22
Tetrominoes:
I = 16, L = 13, O = 21, Z = 29, T = 21
Monomino:
5
You can try it on f-puzzles or penpa-edit
Hint for the break-in (highlight to view): where could the X pentomino go?
Have fun!
matyas
Lösungscode: Column 3
Kommentare
am 22. Oktober 2021, 14:01 Uhr von uvo_mod
Labels angepasst.
am 18. Juni 2021, 02:19 Uhr von cdwg2000
Very good very good! For me, this is definitely a five-star difficulty, because I am relatively new to domino puzzles, and even a unique rectangle appeared in Box1 and Box3 at the end. After inspection, it was found that the numbers on the same domino cannot be eliminated repeatedly.
am 17. Juni 2021, 18:55 Uhr von gigglingCaduceus
Incredible puzzle! It seems ridiculous to me that this has a unique solution, yet there it was!
am 17. Juni 2021, 15:44 Uhr von matt383
Bumped up difficulty to 4*
am 17. Juni 2021, 15:42 Uhr von PjotrV
Tough puzzle, I would disagree with 3 star, I would rate it 4.
But I really loved it for sure!! Amazing puzzle Matyas!
am 16. Juni 2021, 19:15 Uhr von ___
fun concept. enjoyed this a lot
am 16. Juni 2021, 17:56 Uhr von matt383
Added f-puzzles and penpa-edit links.