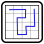
Zehnkampf-100m-Überbleibsel: Persistence of Memory
(Eingestellt am 25. November 2016, 20:00 Uhr von berni)
Lösungscode: Die zweite und die fünfte Zeile von links nach rechts. X für ein Wegfeld und - für ein Leerfeld.
Kommentare
am 28. Juni 2024, 22:02 Uhr von Drawoon
penpa+: https://tinyurl.com/2p2ad6wx
am 4. November 2023, 21:13 Uhr von tretro
The hardest part was to understand the instructions. I.e., not every square of the small areas has to be passed and the way has the width of the squares and is not just a line.
am 29. November 2016, 08:30 Uhr von Eisbär
@ Voyager: That's the thing I was missing, it's a lot easier now :-)) I was a bit confused because there was stated "Feldmiddelpunkt zu Feldmiddelpunkt"...
am 29. November 2016, 03:35 Uhr von Voyager
@Eisbär: Consider the from the path used cells as a snake. Like in usual snake-puzzles this snake is not allowed to touch itself - n.e.d. With this kind of view there is only one solution.
am 29. November 2016, 00:41 Uhr von Eisbär
I think I'm overlooking something... I know there must be just one solution but right now I believe there are several?