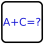Quersummengebiete 3
(Eingestellt am 14. Dezember 2014, 08:00 Uhr von BFaw)
Jedes Gebiet ist durch einen dunkelgrauen Rand begrenzt und hat einen Wert. Dieser kann ermittelt werden, indem alle Zahlen darin summiert werden und dann so lange 'n' abgezogen wird, bis die Zahl kleiner oder gleich 'n' ist.
Benachbarte Gebiete (diagonal zählt nicht) dürfen nicht den gleichen Wert haben. Stimmt der Gebietswert mit einer dem Gebiet benachbarten Zahl (welche sich nicht in diesem befindet) überein, so zeigt ein Pfeil über die entsprechende Gebietsgrenze auf diese Zahl. Alle horizontalen und vertikalen Pfeile sind vorgegeben.
Lösungscode: Für jede Zeile von oben nach unten nur die Einsen und Zweien von links nach rechts; im Beispiel: 2;2;2;1;1;2;1;1;2;2
Kommentare
am 9. Januar 2015, 14:34 Uhr von HaSe
Wirklich tolle Rätsel. Wenn man sich erstmal reingedacht hat, läuft es ganz flüssig, macht Spaß.
am 21. Dezember 2014, 13:53 Uhr von ibag
Die werden immer besser. Irgendwie fällt es mir aber ziemlich schwer, den Überblick zu behalten.
am 21. Dezember 2014, 10:28 Uhr von sandmoppe
Diese Rätselart gefällt mir wirklich gut.
am 17. Dezember 2014, 03:53 Uhr von Rollo
Puh! Gefällt mir immer besser.
am 15. Dezember 2014, 16:58 Uhr von Alex
Super Serie, hat bei mir zu einigem Kopfzerbrechen gefuehrt.
am 14. Dezember 2014, 21:23 Uhr von r45
Sehr schöne Serie, vielen Dank.