Logic Masters Deutschland e.V.

Im ersten Teil haben wir einfache Schlussfolgerungen aus den Zahlenangaben im Rätsel gezogen. Wir kommen nun zu einer weiteren einfachen Schlussfolgerung, die man aus den Zahlen ziehen kann. Wir betrachten die folgenden Situationen.

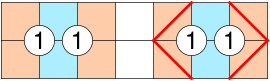Man kann sich leicht überlegen, dass die vier äußeren Felder (im Beispiel rot markiert) nicht zu den 1en gehören. Die Begründung ist, dass die beiden Felder, die von beiden 1en berührt werden (blau markiert), je genau eine Wand zu einer der beiden Zahlen beitragen. Genauso kann man in dem folgenden Beispiel schon vier Wände einzeichnen.

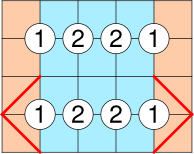
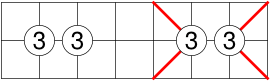Diese Schlussfolgerung kann man verallgemeinern. Wir betrachten eine Kette von Zahlen (damit ist eine lückenlose Reihe von Zahlen gemeint, die alle in derselben Zeile oder Spalte liegen). Die inneren Felder (blau) gehören je genau zu einem Feld mit einer Zahl. Damit können wir über die Summe der Zahlen ausrechnen, wie viele der vier äußeren Felder (blau) zu dieser Kette gehören. Im Beispiel haben wir 6 innere Felder und die Summe der Zahlen ist 6, d.h. von den äußeren Feldern gehört kein Feld zu den Zahlen.

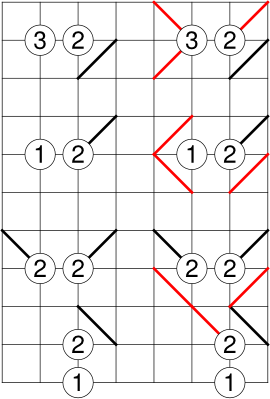
Wenn die Differenz zwischen Anzahl der inneren Felder und Summe der Zahlen 4 oder 0 ergibt, dann lassen sich die äußeren vier Felder direkt mit Wänden füllen. Oft kommen aber auch Ketten vor, bei denen die Differenz dazwischen liegt. Dann kann zwar noch nicht direkt eine Wand eingezeichnet werden, es ist aber möglich im späteren Verlauf des Rätsels daraus Schlussfolgerungen zu ziehen, sobald in die äußeren Felder Wände eingetragen sind. In der folgenden Abbildung sind ein paar Beispiele dafür. Der Rand kann ebenfalls mit in die Ketten einfließen.

Sinnvolle Ketten bestehen in der Mitte übrigens immer aus 2en. Es gibt zwar auch Ketten, die andere Zahlen in der Mitte enthalten. In dem Fall lässt sich aber eine Teilkette finden, die wiederum in der Mitte nur 2en enthält.

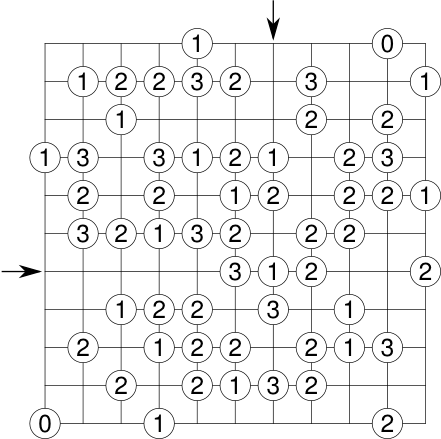
Das folgende Rätsel lässt sich mit der Betrachtung von Ketten (und den Methoden aus dem ersten Abschnitt) lösen.